การคำนวณหาแรงเฉือนและโมเมนต์ดัดในคานแบบง่ายด้วยเครื่องคอมพิวเตอร์แบบกระเป๋า อ่าน 27,878
|
การคำนวณหาแรงเฉือนและโมเมนต์ดัดในคานแบบง่าย วิเคราะห์โครงสร้าง ด้วยเครื่องคอมพิวเตอร์แบบกระเป๋า |
บทนำ
บทความนี้จะอธิบายและแสดงโปรแกรมคอมพิวเตอร์ สำหรับใช้ในการคำนวณค่าแรงเฉือนและโมเมนต์ดัดในคานแบบง่าย (Simple Beam) ซึ่งดัดแปลงมาจากโปรแกรมคอมพิวเตอร์ในหนังสือ Strength of Materials แต่งโดย William A Nash โดยมีวัตถุประสงค์คือ
1. เพื่อแสดงแนวคิดและขั้นตอนวิธี (Algorithm) ในการนำงานที่ใช้การคำนวณด้วยมือไปเป็นการคำนวณด้วยเครื่องคอมพิวเตอร์ได้
2. เพื่อให้นักศึกษามีโปรแกรมคอมพิวเตอร์ที่สามารถ ใช้กับเครื่องคอมพิวเตอร์แบบกระเป๋า (Pocket Computer) เช่น รุ่น FX ของ
คาสิโอ (Casio) หรือรุ่น PC ของชาร์ป (Sharp) ซึ่งทำให้สามารถตรวจคำตอบผลลัพธ์จากการคำนวณด้วยมือได้ด้วยตนเอง
3. ช่วยเสริมความเข้าใจของนักศึกษา ในการศึกษาวิชาพื้นฐานทางวิศวกรรม เช่น วิชากลศาสตร์วิศวกรรม (Engineering Mechanics) วิชาความแข็งแรงของวัสดุ (Strength of Materials)วิชาทฤษฎีโครงสร้าง (Theory of Structures) เป็นต้น
4. เป็นแนวทางในการเขียนโปรแกรมคอมพิวเตอร์ทางด้านวิศวกรรมชั้นสูงต่อไป
ขอบเขตและแนวคิดของโปรแกรม
โปรแกรมคอมพิวเตอร์นี้ สามารถใช้วิเคราะห์หาแรงเฉือนและโมเมนต์ดัดในคาน เมื่อรับน้ำหนักบรรทุกแบบต่างๆเหล่านี้คือ แบบกระทำเป็นจุด (Point Load) แบบโมเมนต์ และแบบแผ่กระจาย (Distributed Load) เชิงเส้นทั้งที่สม่ำเสมอและไม่สม่ำเสมอ อนึ่งแรงปฏิกิริยาถือว่าเป็นน้ำหนักกระทำเป็นจุดด้วย
แนวคิดคือเเบ่งคานออกเป็นชิ้นส่วนย่อย (Segment) ซึ่งด้านซ้ายและด้านขวาของชิ้นส่วนย่อยเรียกว่าตำแหน่ง (Location) ดังภาพที่ 1

แนวทางการแบ่งชิ้นส่วนใดๆนั้น จะพิจารณาจากที่ว่ามีการเปลี่ยนแปลงของน้ำหนักบรรทุกที่กระทำ ณ ตำแหน่งนั้นหรือไม่เป็นหลัก และเนื่องจากผลลัพธ์ที่ได้จากโปรแกรม จะเป็นผลจากแต่ละตำแหน่งด้านซ้ายและด้านขวา ดังนั้นสิ่งที่พิจารณาในการแบ่งชิ้นส่วนย่อย อีกสิ่งหนึ่งคือ เราต้องการค่าของจุดใดบนคาน ก็กำหนดตำแหน่งที่จุดนั้นด้วย
ทิศทาง
ทิศทางที่เป็นบวกของน้ำหนักบรรทุกแสดงดังภาพที่ 2
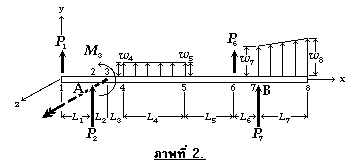
และทิศทางที่เป็นบวกของแรงเฉือนและโมเมนต์ดัด ดังภาพที่ 3
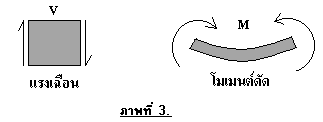
ขั้นตอนวิธีในการคำนวณ
กำหนดสัญลักษณ์ของตัวแปรดังนี้
N = จำนวนชิ้นส่วนย่อยของคานแบบง่าย
S(I) = ความยาวของแต่ละชิ้นส่วนย่อย I พิจารณาจากชิ้นส่วนซ้ายไปขวา โดย I มีค่าตั้งแต่ 1 ถึง N
N1 = จำนวนของน้ำหนักบรรทุกกระทำเป็นจุด (รวมทั้งแรงปฏิกิริยา)
P(I1) = น้ำหนักบรรทุกกระทำเป็นจุดที่ตำแหน่ง I1 โดย I1 มีค่าตั้งแต่ 1 ถึง N1
N2 = จำนวนของโมเมนต์ที่กระทำบนคาน
E(L) = โมเมนต์คู่ควบที่ตำแหน่ง L โดย L มีค่าตั้งแต่ 1ถึง N2
N3 = จำนวนชิ้นส่วนย่อยที่รับน้ำหนักบรรทุกกระจาย
D(N4,1) = ขนาดของน้ำหนักบรรทุกกระจายด้านซ้ายของตำแหน่ง N4 โดย N4 มีค่าตั้งแต่ 1 ถึง N3
D(N4,2) = ขนาดของน้ำหนักบรรทุกกระจายด้านขวาของตำแหน่ง N4 โดย N4 มีค่าตั้งแต่ 1 ถึง N3
V(I,1) = แรงเฉือนด้านซ้ายของตำแหน่ง I โดย I มีค่าตั้งแต่ 1ถึง N+1
V(I,2) = แรงเฉือนด้านขวาของตำแหน่ง I โดย I มีค่าตั้งแต่ 1 ถึง N+1
M(I,1) = โมเมนต์ดัดด้านซ้ายของตำแหน่ง I โดย I มีค่าตั้งแต่ 1 ถึง N+1
M(I,2) = โมเมนต์ดัดด้านขวาของตำแหน่ง I โดยที่ I มี่ค่าตั้งแต่ 1 ถึง N+1
พิจารณาแผนภาพวัตถุอิสระ (Free-body Diagram) ของชิ้นส่วนย่อยที่ 1 นับจากปลายซ้ายของคานดังภาพที่ 4
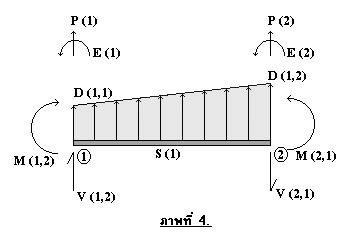
จะได้ว่า
V(1,1) = 0 = M(1,1) (เพราะถือว่าเริ่มที่ด้านขวามือของตำแหน่งที่ 1)
V(1,2) = P(1)
M(1,2) = -E(1)
V(2,1) = V(1,2) + [D(1,1)+D(1,2)]*S(1)/2
M(2,1) = M(1,2) + V(1,2)*S(1) + (2*D(1,2)+D(1,1))*S(1)2/6
พิจารณาแผนภาพวัตถุอิสระของชิ้นส่วนย่อยที่ 2 ดังภาพที่ 5
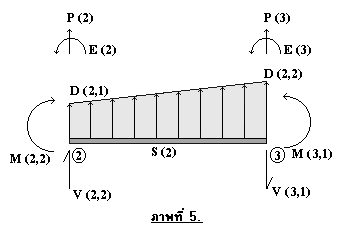
จะได้ว่า
V(2,2) = V(2,1) + P(2)
M(2,2) = M(2,1) + E(2)
V(3,1) = V(2,2) + [D(2,1)+D(2,2)]*S(2)/2
M(3.1) = M(2,2) + V(2,2)*S(2) + [2*D(2,2)+D(2,1)]*S(2)2/6
สำหรับชิ้นส่วนย่อยอื่นๆ ถึงชิ้นส่วนย่อยที่ N ก็คำนวณในทำนองเดียวกันนี้ ซึ่งจะเห็นว่าเราสามารถเขียนโปรแกรมคอมพิวเตอร์ช่วยในการคำนวณโดยใช้การวนซ้ำ (Loop) ช่วงชิ้นส่วนย่อย จะสามารถคำนวณค่าแรงเฉือนและโมเมนต์ดัดทั้งหมดได้
ขั้นตอนวิธีในการหาค่าสูงสุด
เราสามารถเขียนโปรแกรมให้เลือกขนาด (Magnitude) ของแรงเฉือนและโมเมนต์ดัดสูงสุดได้ โดยมีขั้นตอนวิธีดังนี้
1. กำหนดตัวแปร VM และ MM คือ ขนาดของแรงเฉือนและโมเมนต์ดัดสูงสุดตามลำดับ
2. ให้ VM เท่ากับค่าสัมบูรณ์ของแรงเฉือนลำดับแรกคือ V(1,2) และ MM เท่ากับค่าสัมบูรณ์ของโมเมนต์ดัดลำดับแรกคือ M(1,2) (ที่ใช้ค่าสัมบูรณ์เพราะแรงเฉือนและโมเมนต์ดัดเป็นได้ทั้งค่าบวกและลบ ซึ่งเป็นเครื่องหมายแสดงทิศทาง เมื่อหาเฉพาะขนาด จึงไม่คำนึงถึงเครื่องหมาย)
3. วนซ้ำ I = 1 ถึง N โดยที่ N คือจำนวนชิ้นส่วยย่อยทั้งหมด (ABS หมายถึง ค่าสัมบูรณ์)
ถ้า VM < ABS(V(I+1,1)) ให้ VM = ABS(V(I+1,1))
ถ้า VM < ABS(V(I+1,2)) ให้ VM = ABS(V(I+1,2))
ถ้า MM < ABS(M(I+1,1)) ให้ MM = ABS(M(I+1,1))
ถ้า MM < ABS(M(I+1,2)) ให้ MM = ABS(M(I+1,2))
รายละเอียดของโปรแกรมส่วนนี้ คือบรรทัดที่ 360 ถึง 420 ในรายละเอียด (Listing) ของโปรแกรมคอมพิวเตอร์
โปรแกรมคอมพิวเตอร์
โปรแกรมคอมพิวเตอร์นี้ เขียนขึ้นโดยใช้ภาษาเบสิก (BASIC) บนเครื่องคอมพิวเตอร์แบบกระเป๋าของชาร์ป รุ่น PC-1500A โดยกำหนดให้จำนวนชิ้นส่วนย่อยสูงสุดได้ 20 ชิ้นส่วน ดังนั้นจำนวนตำแหน่งสูงสุดจึงเท่ากับ 21 ตำแหน่ง มีรายละเอียดของโปรแกรมดังนี้
10:²A²:CLEAR
20:PAUSE ²SHEAR FORCE²
30:PAUSE ²AND BENDING MOMENT²
40:DIM S(20),P(21),E(21),D(20,2),V(21,2),M(21,2)
50:INPUT ²NUMBER OF SEGMENTS: ²;N
60:PAUSE ²LENGTH OF EACH SEGMENT²
70:PAUSE ²FROM LEFT TO RIGHT²
80:FOR I=1TO N
85:PRINT ²SEGMENT ²+STR$ I
90:INPUT ²S = ²;S(I)
100:NEXT I
110:INPUT ²NO. OF POINT LOADS: ²;N1
120:FOR I=1TO N1
130:INPUT ²LOCATION: ²;I1
140:INPUT :²LOAD: ²;P(I1)
150:NEXT I
160:INPUT ²NO. OF EXT. MOMENTS: ²;N2
170:FOR I=1TO N2
180:INPUT ²LOCATION: ²;L
190:INPUT ²MOMENT: ²;E(L)
200:NEXT I
210:INPUT ²NO. OF DIST. LOAD SEG. ²;N3
220:FOR I=1TO N3
230:INPUT ²SEGMENT NO.: ²;N4
240:INPUT ²LOAD LEFT: ²;D(N4,1)
250:INPUT ²LOAD RIGHT: ²;D(N4,2)
260:NEXT I
270:V(1,2)=P(1)
280:M(1,2)=-E(1)
290:FOR I=1TO N
300:V(I+1,1)=V(I,2)+(D(I,1)+D(I,2))*S(I)/2
310:V(I+1,2)=V(I+1,1)+P(I+1)
320:T2=((2*D(I,1)+D(I,2))*S(I)^2)/6
330:M(I+1,1)=M(I,2)+V(I,2)*S(I)+T2
340:M(I+1,2)=M(I+1,1)-E(I+1)
350:NEXT I
360:VM=ABS (V(1,2))
365:MM=ABS (M(1,2))
370:FOR I=1TO N
380:IF VM
390:IF VM
400:IF MM
410:IF MM
420:NEXT I
430:FOR I=1TO N+1
440:PRINT ²LOCATION ²+STR$ I
450:PRINT ²SHEAR LEFT = ²+STR$ V(I,1)
460:PRINT ²SHEAR RIGHT = ²+STR$ V(I,2)
470:PRINT ²MOMENT LEFT = ²+STR$ M(I,1)
480:PRINT ²MOMENT RIGHT = ²+STR$ M(I,2)
490:NEXT I
500:PRINT "Vmax.(mag.) = "+STR$ VM
510:PRINT "Mmax.(mag.) = "+STR$ MM
520:END
ตัวอย่างการคำนวณ
คานแบบง่ายรับน้ำหนักบรรทุกดังภาพที่ 6
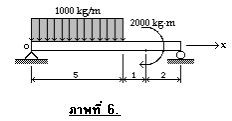
จากการคำนวณด้วยมือ สามารถเขียนแผนภาพแรงเฉือนและโมเมนต์ดัดได้ดังภาพที่ 7
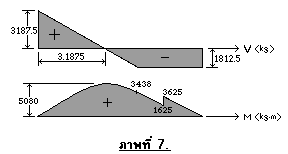
ในการกำหนดข้อมูลป้อนเข้า (Input) ของโปรแกรม มีข้อพิจารณาคือ กำหนดตำแหน่งซึ่งมีน้ำหนักบรรทุกกระทำ และตำแหน่งที่ต้องการทราบค่าแรงเฉือนและโมเมนต์ดัด จึงกำหนดดังภาพที่ 8
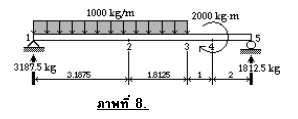
เพราะฉะนั้น
จำนวนชิ้นส่วนย่อย = 4
จำนวนตำแหน่ง = 5
จำนวนชิ้นส่วนรับน้ำหนักกระ



