การพัฒนาโปรแกรมคอมพิวเตอร์ทางด้านกราฟิกสำหรับแสดงแผนภาพการวิเคราะห์คาน อ่าน 8,031

วิเคราะห์โครงสร้าง

การพัฒนาโปรแกรมคอมพิวเตอร์ทางด้านกราฟิก

สำหรับแสดงแผนภาพการวิเคราะห์คาน

บทนำ

จากบทความเรื่อง การคำนวณหาแรงเฉือนและโมเมนต์ดัดในคานแบบง่าย ด้วยเครื่องคอมพิวเตอร์แบบกระเป๋า ที่ผู้เขียนนำเสนอ [1] และได้ให้ข้อเสนอแนะว่าควรพัฒนาโปรแกรมบนไมโครคอมพิวเตอร์ โดยเพิ่มการแสดงผลทางกราฟิก ผู้เขียนจึงนำมาอธิบายในตอนนี้ โดยเปลี่ยนจากพัฒนาบนเครื่องคอมพิวเตอร์แบบกระเป๋าเป็นบนไมโครคอมพิวเตอร์ และเปลี่ยนจากภาษาเบสิก (BASIC) เป็นเทอร์โบปาสกาล (Turbo Pascal) เนื่องจากมีประสิทธิภาพดีกว่าในการแสดงผลทางกราฟิก ดังนั้น การนำเสนอในตอนนี้ จะเน้นที่การแสดงผลทางกราฟิก ส่วนการคำนวณยังใช้ขั้นตอนวิธี (Algorithm) เหมือนเดิม สามารถดูรายละเอียดได้จากวารสารเล่มดังกล่าว

ทบทวนแนวคิดเดิม

แนวคิดในการวิเคราะห์คานคือ แบ่งคานออกเป็นชิ้นส่วนย่อย (Segment) ซึ่งด้านซ้ายและด้านขวาของชิ้นส่วนย่อยเรียกว่าตำแหน่ง (Location) ดังภาพที่ 1

ทิศทางที่เป็นบวกของน้ำหนักบรรทุกแสดงดังภาพที่ 2

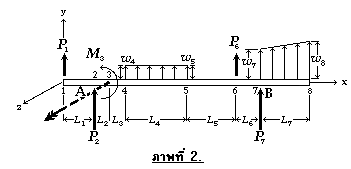
และทิศทางที่เป็นบวกของแรงเฉือนและโมเมนต์ดัด ดังภาพที่ 3

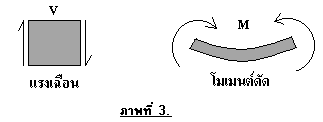
ผังงานของโปรแกรม

ผังงาน (Flowchart) ของโปรแกรม แสดงดังภาพที่ 4

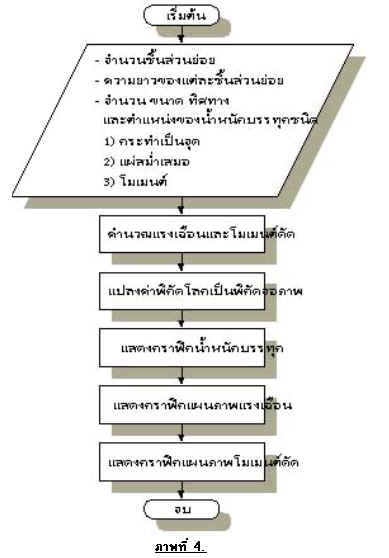
การแปลงพิกัด

ในการแสดงผลทางกราฟิกของคานซึ่งเกิดจากค่าในการคำนวณ ให้ปรากฎที่หน้าจอคอมพิวเตอร์ เราไม่สามารถใช้หน่วยนั้นๆ ให้แสดงที่หน้าจอได้ทันที เพราะหน่วยที่จอภาพเป็นหน่วยที่เรียกว่าจุดภาพ (Pixel) จึงต้องทำการแปลงพิกัด ซึ่งเรียกว่า การแปลงพิกัดโลก (World Coordinate) ให้เป็นพิกัดจอภาพ (Screen Coordinate) แนวคิดที่ผู้เขียนใช้คือ (พิจารณาภาพที่ 5)

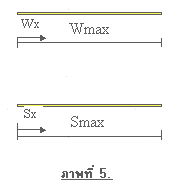
กำหนดให้

W_max = ระยะสูงสุดในพิกัดโลก (m)

S_max = ระยะสูงสุดในพิกัดจอภาพ (pixel)

W_x = ระยะใดๆ ในพิกัดโลก (m)

S_x = ระยะใดๆ ในพิกัดจอภาพ (pixel)

k = ค่าคงที่ในการแปลง

จะได้ว่า

ให้ W_max เทียบได้กับ S_max

ดังนั้น W_x เทียบได้กับ W_x · (S_max / W_max)

หรือ S_x = W_x · k

โดยที่ k = S_max / W_max

ซึ่งในโปรแกรม จะมีการแปลงค่าต่างๆ คือ

1. การแปลงพิกัดความยาวคาน มีขั้นตอนวิธีดังนี้

1.1 รวมความยาวชิ้นส่วนย่อยทั้งหมดเป็นความยาวคาน

1.2 หาค่าคงที่ในการแปลง ซึ่งเท่ากับความยาวคาน/ระยะสูงสุดในหน่วยจุดภาพที่กำหนด

1.3 แปลงพิกัดความยาวของชิ้นส่วนย่อยใดๆ ทั้งหมด

2. การแปลงน้ำหนักบรรทุกชนิดแผ่สม่ำเสมอ (Uniform Load) มีขั้นตอนวิธีดังนี้

2.1 วนซ้ำ (Loop) แต่ละชิ้นส่วนย่อย เพื่อหาขนาดของน้ำหนักที่มากที่สุด

2.2 หาค่าคงที่ในการแปลง ซึ่งเท่ากับ ขนาดของน้ำหนักที่มากที่สุด/ระยะสูงสุดในหน่วยจุดภาพที่กำหนด

2.3 แปลงพิกัดน้ำหนักที่มีในแต่ละชิ้นส่วนย่อย

สำหรับการแปลงพิกัดแรงเฉือนและโมเมนต์ดัด ก็ทำในทำนองเดียวกันกับข้อ 2

การแสดงกราฟิกที่จอภาพ

เมื่อได้พิกัดจอภาพแล้ว ก็สามารถสร้างกราฟิกได้ คล้ายกับการลากเส้นด้วยมือ แต่ทำอย่างเป็นระบบ ซึ่งมีขั้นตอนวิธีดังนี้

1. กำหนดให้สร้างกราฟิกจากซ้ายไปขวา

2. กำหนดลงจุดเริ่มต้นที่พิกัดด้านซ้ายสุด

3. ใช้การวนซ้ำ ลากเส้นต่อทีละจุด จนไปถึงพิกัดด้านขวาสุด

มีข้อควรระวัง ในกรณีใช้เทคนิคนี้คือ เนื่องจากทิศทางในจอภาพนั้นคว่ำลง คือเริ่มต้นพิกัด (0,0) ที่มุมบนซ้าย และพิกัดสูงสุดที่มุมล่างขวา ดังนั้น ในการกำหนดตำแหน่ง จะต่างจากพิกัดโลก เช่น ค่าแรงเฉือนเป็นบวก แต่การกำหนดพิกัดในจอภาพต้องเป็นลบ

โปรแกรมคอมพิวเตอร์

โปรแกรมคอมพิวเตอร์ เขียนขึ้นโดยใช้ตัวแปลภาษาเทอร์โบปาสกาล รุ่น 7.0 มีรหัสต้นฉบับ (Source Code) ดังนี้ (หมายเลขข้างหน้า เป็นการกำหนดเพื่ออ้างอิงในการเขียนบทความเท่านั้น)

001: Program Beam;

002: Uses Crt, Graph;

003: Const

004: Lsr = 250;

005: X1 = 50; X2 = 300;

006: Yf = 100;

007: Ys = 250;

008: Ym = 400;

009: MaxU = 20;

010: MaxS = 50; MaxM = 50;

011: Var

012: N1, I1, N2, L, N3, N4 : Byte;