ปัดฝุ่น 03 : “สมการสมดุลย์” คุณว่า..มาจากใหน..แล้วใยต้องเป็น 3 หรือ 6” อ่าน 8,966

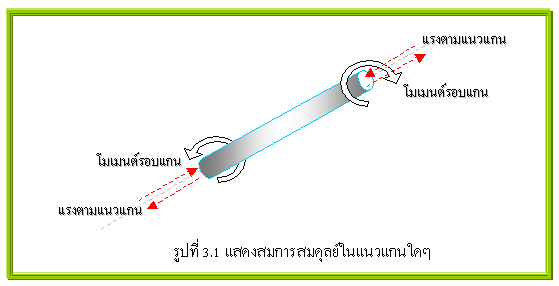
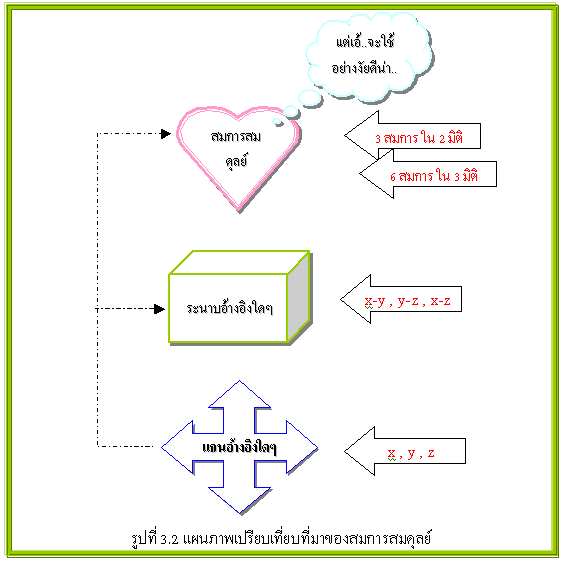
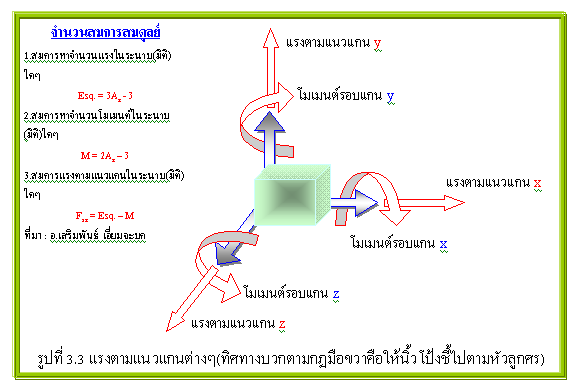
การแก้สมการใดๆทางคณิตศาสตร์ “จำนวนสมการจะต้องมีมากกว่าหรือเท่ากับตัวแปรที่ยังไม่ทราบค่า” ประโยคนี้เราๆท่านๆรู้และท่อง(คับคล้ายคับว่าออกจะเหมือน...นกแก้วนกขุนทอง)กันตั้งแต่เข้าวงการ(เข้าโรงเรียน)ได้ไม่นานมั้ง แต่เอาหล่ะ..นั่นเป็นประเด็นพื้นฐานหลัก ในการแก้สมการโจทย์ทางการคำนวณในศาสตร์แขนงต่างๆ

ที่นี้ย้อนกลับมามอง(ศาสตร์และศิลป์ใน)การวิเคราะห์โครงสร้างทางวิศวกรรมโยธาบ้าง ในกระบวนการดังกล่าวก็คือลำดับขั้นตอนในการแก้สมการทางคณิตศาสร์เช่นเดียวกัน ฉะนั้นหลักพื้นฐานเบื้องตนในการแก้สมการก็ต้องยึดหลักดังกล่าวข้างต้นเหมือนกัน แต่..มีสิ่งที่น่าสังเกตอย่างหนึ่งว่า “ในการวิคราะห์โครงสร้างนั้น..จำนวนสมการหลักๆ(ยังไม่รวมสมการเสริมสภาพคล้องทั้งหลายแหล่นะครับ)จะขึ้นอยู่กับระบบของแกนอ้างอิง หรือกล่าวอีกนัยหนึ่งคือขึ้นอยู่กับมิติมุมมองในการจำลองโครงสร้างเป็นเกณฑ์(ดูรูปที่ 3.2 ประกอบครับ)” ซึ่งแกนอ้างอิงหรือมิติมุมมองต่างๆดังกล่าวนั้น(โดยทั่วไปเรามองว่ามีเพียง 2 มิติ และ 3 มิติ เท่านั้น) ประกอบขึ้นจาก “ระนาบใดๆ(plane)” มาประสานเข้าด้วยกัน(ซึ่งตรงนี้หล่ะครับ..จะเกิดการซ้อนทับของตัวแปรและสมการสมดุลย์..ทำให้เกิดการลด-ทอนตัวแปรและสมการสมดุลย์ลงได้ครึ่งหนึ่งเสมอ) และระนาบใดๆก็ประกอบขึ้นจาก “แนวแกนอ้างอิงใดๆ(axis)” มาเชื่อมต่อกัน โดยการเชื่อมและประสานดังกล่าว(สมมุติว่าเป็น)วางตัวเป็นไปในลักษณะของมุมฉาก(ทฤษฎีจ๋าครับ)

เอาหล่ะ...ที่นี้ แล้วใน 2 มิติ มีกี่สมการ(เกี่ยวกับตัวแปรหรือแรงใดบ้าง) และใน 3 มิติ มีกี่สมการ(เกี่ยวกับตัวแปรหรือแรงใดบ้าง)...แต่ก่อนอื่นขอให้ทำความเข้าใจก่อนว่า(ดูรูปที่ 3.1 และ 3.3 ประกอบครับ) “แนวแกนใดๆใน 3 มิติ(ที่อิสระ) ให้ถือว่ามีสมการสมดุลย์เพียง 2 สมการเท่านั้นคือ สมการสมดุลย์ของแรงตามแนวแกน 1 สมการ(อันเนื่องมาจากแรงต่างที่กระทำในแนวแกนนั้น) และสมการสมดุลย์ของโมเมนต์รอบแนวแกนอันเนื่องมาจากการกระทำของแรงในแนวแกนอื่น(2 แนวแกนที่เหลือ)ที่ตั้งฉากกับแนวแกนดังกล่าวอีก 1 สมการ” แต่ “การยุบบางแกนทิ้ง(กรณี 2 มิติ)” และ “การประสานแกนเข้าด้วยกัน(กรณี 3 มิติ)” จะทำให้เกิดการลด-ทอนสมการสมสมดุลย์ลงโดยอัตโนมัติ ขอให้สังเกตให้ดีว่า(ในตอนนี้)ผมจะใช้คำว่าแรงตามแนวแกนเฉยๆ(โดยไม่ระบุลงไปเลยว่าเป็นแรงอัด-ดึง หรือแรงเฉือน) และใช้คำว่าโมเมนต์หมุนรอบแนวแกนเฉยๆ(โดยไม่ระบุลงไปเลยว่าโมเมนต์ดัด หรือโมเมนต์บิด) ทั้งนี้เนื่องจากว่าการที่เราจะเรียกแรงต่างๆ(แรงตามแนวแกนและโมเมนต์)ว่าเป็นแรงใดได้นั้น(แรงอัด,แรงดึง,แรงเฉือน,โมเมนต์ดัด และโมเมนต์บิด) จักต้องทำความเข้าใจในระบบของแกนอ้างอิงให้ดีเสียก่อน(ผมเขียนไว้ใน “ปัดฝุ่น04”)

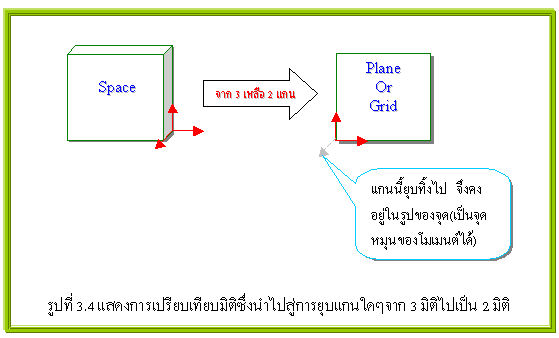
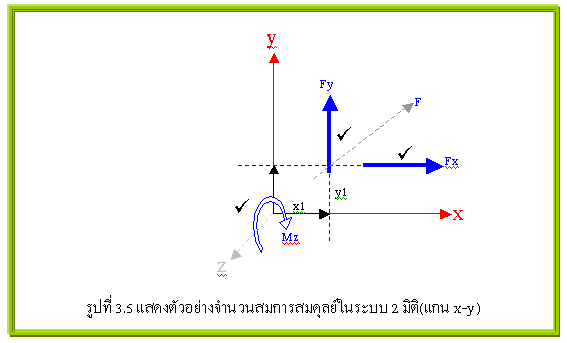
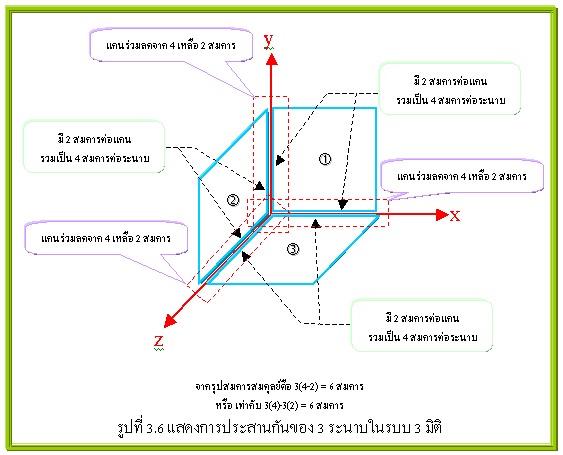
 ในระบบ 2 มิติ(เฉพาะ In Plane หรือ ระนาบ ไม่รวม ระบบกริด) : ซึ่งอาจจะเป็นระนาบ x-y(แกน x ต่อกับแกน y ซึ่งควรจะมีสมการสมดุลย์ 4 สมการตามที่เขียนไว้ด้านบน..แต่..ทำไมจึงมีแค่ 3 สมการ..อ่านต่อไปครับ) , y-z(นี่ก็เช่นเดียวกัน) หรือ x-z(นี่ก็เช่นเดียวกัน) แต่..ประเด็นมันอยู่ที่ว่าในสภาพความเป็นจริงนั้นโครงสร้างจะอยู่ในสภาพ 3 มิติ แต่ทว่าในบางกรณีนั้นเราก็สามารถที่จะยุบมิติ(แนวแกน)ในบางทิศทางให้เหลือเพียง 2 มิติได้ เมื่อระยะในมิติ(แนวแกนใดๆ)ใดเมื่อเทียบกับระยะในอีก 2 มิติ(แนวแกน)ที่เหลือแล้ว มีค่าน้อยมากจนให้ถือว่าเป็นศูนย์(ดูรูปที่ 3.4 ประกอบครับ) เช่น แผ่นกระดาษ แผ่นกระดานดำ ฯล ซึ่งจากเงื่อนไขดังกล่าวนี้(เพื่อความเข้าใจให้ดูรูปที่ 3.5 ประกอบ..ซึ่งเป็นตัวอย่างในระบบแกน x-y)ทำให้แรงที่ขนานกับแนวแกน ไม่สามารถพัฒนาตัวเองไปสู่โมเมนต์ให้หมุนรอบแนวแกนทั้ง 2 ของตนเองได้ เนื่องจากแขนของโมเมนต์เป็นศูนย์(ตามรูปที่ 3.5 แขนของโมเมนต์คือ ระยะตามแนวแกน z ซึ่งถูกยุบไปจึงเป็นศูนย์) แต่กลับทำให้เกิดโมเมนต์หมุนรอบแนวแกน z ทั้งหมดแทน(จึงสามารถใช้สมการสมดุลย์ของโมเมนต์รอบแกน z เพียงสมการเดียวได้ ในที่นี้ตามรูป 3.5 คือ åMz = 0)คือ Mz = Fx*y1 และ Mz = Fy*x1 ในขณะที่ในแต่ละแนวแกนก็จะมีแรงกระทำตามแนวแกนนั้นๆแยกโดยอิสระจากกัน(ส่วนแนวแกนที่ยุบไปเป็นไปไม่ได้ที่จะมีแรงมากระทำ จึงเหลือสมการสมดุลย์ของแรงเพียง 2 สมการใน 2 แนวแกนที่เหลือในที่นี้ตามรูป 3.4 คือ åFx = 0 และ åFy = 0)คือ Fx และ Fy ดังนั้นกล่าวโดยสรุป สมการสมดุลย์ของแรงในโครงสร้างระบบระนาบ(หรือระบบ 2 มิติ)จึงมีเพียง 1.สมการสมดุลย์ของแรงตามแนวแกนทั้งสอง(In Plane…โดยตัดสมการของแรงตามแนวแกนที่ยุบทิ้งไปเพราะไม่มีแนวแกนที่จะดุลย์สมการได้) 2 สมการ 2.สมการสมดุลย์ของโมเมนต์ที่หมุนรอบจุด(หมุน)ของแกนที่ยุบทิ้งไปอีก 1 สมการ ทั้งหมดรวมเป็น 3 สมการ

 ในระบบ 3 มิติ(Space หรือ อวกาศ) : ซึ่งเกิดจากระบบแกนในระนาบ 3 ระนาบมาประสานกันในแนวตั้งฉากคือ x-y , y-z และ x-z นั้นหมายความว่าไม่มีการยุบในแนวแกนใดๆ ดังนั้นในแต่ละแนวแกนจึงอิสระ ทำให้มีสมการสมดุลย์คงอยู่อย่างสมบูรณ์นั้นคือ 2 สมการต่อแนวแกน และเมื่อแต่ละแนวแกนมาต่อเชื่อมกันเป็นระนาบ(2 มิติ) ก็จะทำให้มีสมการสมดุลย์ 2*2 = 4 สมการต่อระนาบ และในขณะเดียวกันเมื่อนำระนาบ 3 ระนาบมาประสานกัน(วางในแนวที่ตั้งฉากกัน) ซึ่งจะทำให้มีสมการสมดุลย์ 3*(2*2) = 12 สมการ แต่ทำไมถึงบอกว่ามีเพียง 6 สมการ ซึ่งสามารถอธิบายได้ดังนี้คือ เมื่อ 3 ระนาบมาประสานกัน(ดูรูปที่ 3.6 ประกอบ)จะเห็นว่ามีอยู่ 3 แนวแกนที่แต่ละระนาบมาประสานหรือเชื่อมเข้าด้วยกัน(ในรูปที่ 3.6 ก็คือบริเวณที่กรอบสี่เหลี่ยมไข่ปลาครอบอยู่) ซึ่งในแต่ละแนวแกนที่ 2 ระนาบมาประสานเข้าด้วยกัน ก็จะได้สมการสมดุลย์ 4 สมการต่อแนวแกนที่ประสานกัน(ถ้าไม่ประสานจะเป็น 2 สมการต่อแนวแกน) แต่เพราะด้วยเหตุการ “การประสานแกน” ดังกล่าว จึงทำให้สมการสมดุลย์ 4 สมการต่อแนวแกนที่ประสานกันใช้ร่วมกันได้ ดังนั้นจึงสามารถลดสมการสมดุลย์จาก 4 มาเหลือ 2 สมการต่อแนวแกนที่ประสานกัน ดังนั้นสมการสมดุลย์ในระบบ 3 มิติจึงมีค่าเท่ากับ 3*(2*2) -3(2) = 6 สมการ ดังนั้นกล่าวโดยสรุป สมการสมดุลย์ของแรงในโครงสร้างระบบ 3 มิติ(Space หรืออวกาศ)จึงมีเพียง 1.สมการสมดุลย์ของแรงตามแนวแกนทั้งสองสาม 3 สมการ 2.สมการสมดุลย์ของโมเมนต์ที่หมุนรอบแกนแกนทั้ง 3 อีก 3 สมการ ทั้งหมดรวมเป็น 6 สมการ